Keywords: glm | regression | poisson regression | link-function | zero-inflated | mixture model | bayesian workflow | Download Notebook
Contents
- Monks working on manuscripts
- First model: just do a simple poisson
- A second model: 0 inflated poisson
- In search of a better model
%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib as mpl
import matplotlib.cm as cm
import matplotlib.pyplot as plt
import pandas as pd
pd.set_option('display.width', 500)
pd.set_option('display.max_columns', 100)
pd.set_option('display.notebook_repr_html', True)
import seaborn as sns
sns.set_style("whitegrid")
sns.set_context("poster")
import pymc3 as pm
//anaconda/envs/py3l/lib/python3.6/site-packages/h5py/__init__.py:34: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
from ._conv import register_converters as _register_converters
Monks working on manuscripts
From McElreath:
Now imagine that the monks take breaks on some days. On those days, no manuscripts are completed. Instead, the wine cellar is opened and more earthly delights are practiced. As the monastery owner, you’d like to know how often the monks drink. The obstacle for inference is that there will be zeros on honest non-drinking days, as well, just by chance. So how can you estimate the number of days spent drinking?

The kind of model used to solve this problem is called a Mixture Model. We’ll see these in more detail next week, but here is a simple version that arises in Poisson regression.
Let $p$ be the probability that the monks spend the day drinking, and $\lambda$ be the mean number of manuscripts completed, when they work.
Likelihood
The likelihood of observing 0 manuscripts produced is is:
\[\cal{L}(y=0) = p + (1-p) e^{-\lambda},\]since the Poisson likelihood of $y$ is $ \lambda^y exp(–\lambda)/y!$
Likelihood of a non-zero $y$ is:
\[\cal{L}(y \ne 0) = (1-p) \frac{\lambda^y e^{-\lambda}}{y!}\]This model can be described by this diagram, taken from Mc-Elreath
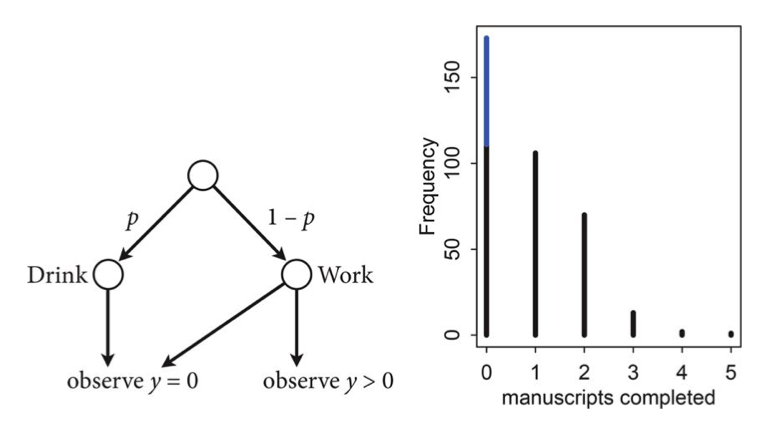
Generating the data
We’re throwing bernoullis for whether a given day in the year is a drinking day or not…
from scipy.stats import binom
p_drink=0.2
rate_work=1
N=365
drink=binom.rvs(n=1, p=p_drink, size=N)
drink
array([0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1,
0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1,
0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0,
1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1,
0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1,
0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1,
1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0,
0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1,
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0])
On days we dont drink, we produce some work…though it might be 0 work…
from scipy.stats import poisson
y = ( 1 - drink)*poisson.rvs(mu=rate_work, size=N)
y
array([1, 0, 0, 1, 1, 2, 0, 0, 0, 0, 0, 1, 0, 1, 0, 2, 0, 4, 0, 1, 0, 0,
0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 3, 0, 1, 0, 0, 0, 0, 3,
0, 0, 0, 0, 0, 1, 1, 4, 1, 1, 2, 1, 3, 0, 1, 2, 2, 1, 1, 2, 1, 0,
0, 2, 3, 1, 1, 2, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 2,
1, 2, 2, 1, 2, 0, 1, 0, 1, 1, 3, 1, 0, 2, 1, 1, 0, 1, 0, 1, 0, 0,
0, 0, 0, 0, 0, 3, 1, 0, 0, 0, 3, 0, 0, 0, 0, 2, 1, 1, 1, 0, 2, 0,
0, 0, 0, 1, 1, 0, 2, 0, 2, 1, 1, 2, 0, 0, 0, 0, 2, 1, 0, 0, 1, 1,
0, 0, 0, 0, 0, 1, 2, 1, 0, 0, 1, 1, 2, 0, 0, 2, 1, 2, 0, 0, 2, 0,
1, 0, 0, 0, 0, 0, 0, 2, 0, 3, 0, 1, 0, 0, 0, 1, 1, 0, 0, 2, 1, 0,
3, 0, 2, 0, 3, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0,
0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 2, 1, 1, 0, 0, 2, 0, 0, 0, 0, 4,
0, 2, 0, 0, 1, 4, 2, 0, 1, 1, 0, 1, 1, 2, 3, 0, 0, 0, 0, 0, 0, 1,
2, 2, 0, 0, 1, 0, 1, 1, 2, 2, 2, 1, 1, 0, 1, 1, 0, 2, 1, 1, 0, 3,
0, 1, 3, 0, 0, 3, 1, 1, 1, 2, 2, 0, 1, 0, 2, 1, 0, 1, 0, 0, 1, 2,
3, 1, 0, 0, 0, 0, 1, 3, 0, 2, 0, 2, 2, 1, 0, 4, 0, 0, 0, 0, 2, 0,
3, 0, 0, 0, 0, 1, 0, 0, 1, 1, 2, 1, 2, 3, 2, 0, 1, 0, 2, 0, 2, 0,
1, 0, 1, 0, 2, 0, 0, 3, 1, 1, 2, 0, 2])
Lets manufacture a histogram of manuscripts produced in a day.
zeros_drink=np.sum(drink)
a=drink==0
b=y==0
zeros_work=np.sum(a & b)
zeros_drink, zeros_work, np.sum(b)
(76, 107, 183)
plt.hist(zeros_work*[0], bins=np.arange(10))
plt.hist(y, bins=np.arange(10), alpha=0.5)
(array([183., 104., 54., 19., 5., 0., 0., 0., 0.]),
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
<a list of 9 Patch objects>)
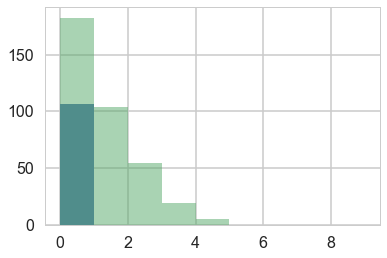
Lets throw in some domain expertise
A survey of Abbey Heads has told us, that the most a monk could produce, ever, was 10 manuscripts in a day.
First model: just do a simple poisson
import theano.tensor as t
def model_poisson(observed=False):
with pm.Model() as model:
lam=pm.HalfNormal("lambda", 100)
like = pm.Poisson("obsv", mu=lam, observed=observed)
return model
model0 = model_poisson(observed=y)
with model0:
trace0=pm.sample(3000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Sampling 2 chains: 100%|██████████| 7000/7000 [00:02<00:00, 2551.34draws/s]
The acceptance probability does not match the target. It is 0.8826517317809268, but should be close to 0.8. Try to increase the number of tuning steps.
The acceptance probability does not match the target. It is 0.8823970764263942, but should be close to 0.8. Try to increase the number of tuning steps.
pm.traceplot(trace0)
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_base.py:3604: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
alternative='`bottom`', obj_type='argument')
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x12456cd68>,
<matplotlib.axes._subplots.AxesSubplot object at 0x1263975f8>]],
dtype=object)

pm.summary(trace0)
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| lambda | 0.794177 | 0.046064 | 0.001038 | 0.704709 | 0.884261 | 2167.755813 | 1.001699 |
from scipy import stats
lbda = np.linspace(0, 200, num=1000)
normpdf = stats.norm(loc=0,scale=100).pdf(lbda)
plt.plot(lbda, normpdf, lw=2)
plt.xlabel("lambda");
plt.ylabel("Prior Density");
plt.fill_between(lbda,0.,normpdf)
plt.axvline(10, 0 ,1, c="r", lw=3);
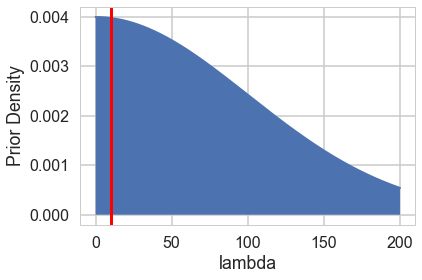
Some proper workflow
Notice the prior specification though: at the 3$\sigma$ level, $\lambda$ could range from 0 to 300, ie from 0 to an extremely large number to an extremely large “mean” of counts. Not possible. Indeed, the max count is around 10. For a poisson, since the variance is equal to the mean, this means that (at 3$\sigma):
\[max(\lambda + 3\sqrt{\lambda}) < 10\]Any prior should only take us marginally outside this range:
4+3*np.sqrt(4)
10.0
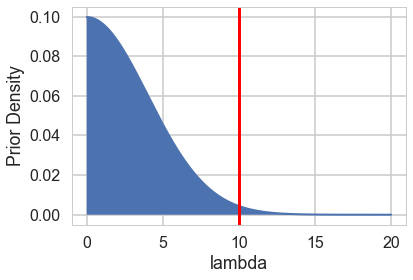
from scipy import stats
lbda = np.linspace(0, 20, num=1000)
normpdf = stats.norm(loc=0,scale=4).pdf(lbda)
plt.plot(lbda, normpdf, lw=2)
plt.xlabel("lambda");
plt.ylabel("Prior Density");
plt.fill_between(lbda,0.,normpdf)
plt.axvline(10, 0 ,1, c="r", lw=3);
pois = stats.poisson.rvs(stats.halfnorm(scale=4).rvs(1000))
plt.hist(pois)
(array([366., 281., 171., 54., 65., 35., 10., 10., 6., 2.]),
array([ 0. , 1.7, 3.4, 5.1, 6.8, 8.5, 10.2, 11.9, 13.6, 15.3, 17. ]),
<a list of 10 Patch objects>)
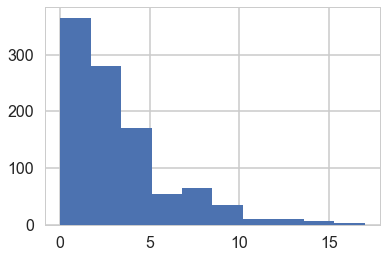
np.mean(pois > 10)
0.028
Limiting the prior
Thus a prior should mainly limit $\lambda$ to values upto 4. To so this consider:
from scipy.stats import halfnorm
halfnorm.ppf(0.99, loc=0,scale=4)
10.303317214195602
def model_poisson1(sd, datasize, observed=False):
with pm.Model() as model:
lam=pm.HalfNormal("lambda", sd)
like = pm.Poisson("obsv", mu=lam, shape = datasize, observed=observed)
return model
Simulating the Bayesian Joint distribution
This should be way enough!, So lets go again:
N = y.shape[0]
N
365
model1_pr = model_poisson1(4, N, observed=None)
with model1_pr:
trace1_pr = pm.sample_prior_predictive(500)
trace1_pr['lambda'].shape, trace1_pr['obsv'].shape
((500,), (500, 365))
plt.hist(trace1_pr['lambda']);
simy = trace1_pr['obsv']
simu_lbdas = trace1_pr['lambda']
simu_lbdas.shape, simy.shape
((500,), (500, 365))
simu_lbdas = stats.halfnorm(scale=4).rvs(500)
simy = np.zeros((500, y.shape[0]))
for i in range(500):
simy[i,:] = stats.poisson(simu_lbdas[i]).rvs(y.shape[0])
x_max = 21
bins = np.arange(0,x_max)
hists = np.apply_along_axis(lambda a: np.histogram(a, bins=bins)[0], 1, simy)
hists.shape #500 rows with 20 cols
(500, 20)
np.linspace(10,90,num=9, dtype=int)
array([10, 20, 30, 40, 50, 60, 70, 80, 90])
prctiles = np.percentile(hists,np.linspace(10,90,num=9, dtype=int),axis=0)
bin_interp = np.linspace(0,x_max-1,num=(x_max-1)*10)
bin_interp
array([ 0. , 0.10050251, 0.20100503, 0.30150754, 0.40201005,
0.50251256, 0.60301508, 0.70351759, 0.8040201 , 0.90452261,
1.00502513, 1.10552764, 1.20603015, 1.30653266, 1.40703518,
1.50753769, 1.6080402 , 1.70854271, 1.80904523, 1.90954774,
2.01005025, 2.11055276, 2.21105528, 2.31155779, 2.4120603 ,
2.51256281, 2.61306533, 2.71356784, 2.81407035, 2.91457286,
3.01507538, 3.11557789, 3.2160804 , 3.31658291, 3.41708543,
3.51758794, 3.61809045, 3.71859296, 3.81909548, 3.91959799,
4.0201005 , 4.12060302, 4.22110553, 4.32160804, 4.42211055,
4.52261307, 4.62311558, 4.72361809, 4.8241206 , 4.92462312,
5.02512563, 5.12562814, 5.22613065, 5.32663317, 5.42713568,
5.52763819, 5.6281407 , 5.72864322, 5.82914573, 5.92964824,
6.03015075, 6.13065327, 6.23115578, 6.33165829, 6.4321608 ,
6.53266332, 6.63316583, 6.73366834, 6.83417085, 6.93467337,
7.03517588, 7.13567839, 7.2361809 , 7.33668342, 7.43718593,
7.53768844, 7.63819095, 7.73869347, 7.83919598, 7.93969849,
8.04020101, 8.14070352, 8.24120603, 8.34170854, 8.44221106,
8.54271357, 8.64321608, 8.74371859, 8.84422111, 8.94472362,
9.04522613, 9.14572864, 9.24623116, 9.34673367, 9.44723618,
9.54773869, 9.64824121, 9.74874372, 9.84924623, 9.94974874,
10.05025126, 10.15075377, 10.25125628, 10.35175879, 10.45226131,
10.55276382, 10.65326633, 10.75376884, 10.85427136, 10.95477387,
11.05527638, 11.15577889, 11.25628141, 11.35678392, 11.45728643,
11.55778894, 11.65829146, 11.75879397, 11.85929648, 11.95979899,
12.06030151, 12.16080402, 12.26130653, 12.36180905, 12.46231156,
12.56281407, 12.66331658, 12.7638191 , 12.86432161, 12.96482412,
13.06532663, 13.16582915, 13.26633166, 13.36683417, 13.46733668,
13.5678392 , 13.66834171, 13.76884422, 13.86934673, 13.96984925,
14.07035176, 14.17085427, 14.27135678, 14.3718593 , 14.47236181,
14.57286432, 14.67336683, 14.77386935, 14.87437186, 14.97487437,
15.07537688, 15.1758794 , 15.27638191, 15.37688442, 15.47738693,
15.57788945, 15.67839196, 15.77889447, 15.87939698, 15.9798995 ,
16.08040201, 16.18090452, 16.28140704, 16.38190955, 16.48241206,
16.58291457, 16.68341709, 16.7839196 , 16.88442211, 16.98492462,
17.08542714, 17.18592965, 17.28643216, 17.38693467, 17.48743719,
17.5879397 , 17.68844221, 17.78894472, 17.88944724, 17.98994975,
18.09045226, 18.19095477, 18.29145729, 18.3919598 , 18.49246231,
18.59296482, 18.69346734, 18.79396985, 18.89447236, 18.99497487,
19.09547739, 19.1959799 , 19.29648241, 19.39698492, 19.49748744,
19.59798995, 19.69849246, 19.79899497, 19.89949749, 20. ])
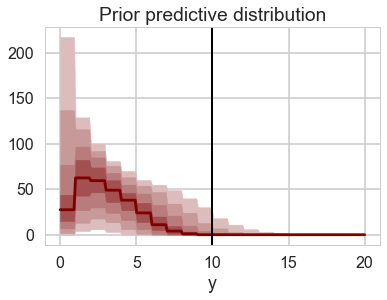
prctiles_interp = np.repeat(prctiles, 10,axis=1)
c_light ="#DCBCBC"
c_light_highlight ="#C79999"
c_mid ="#B97C7C"
c_mid_highlight ="#A25050"
c_dark ="#8F2727"
c_dark_highlight ="#7C0000"
for i,color in enumerate([c_light,c_light_highlight,c_mid,c_mid_highlight]):
plt.fill_between(bin_interp,prctiles_interp[i,:],prctiles_interp[-1-i,:],alpha=1.0,color=color);
plt.plot(bin_interp,prctiles_interp[4,:],color=c_dark_highlight);
plt.axvline(x=10,ls='-',lw=2,color='k');
plt.xlabel('y');
plt.title('Prior predictive distribution');
plt.plot(simu_lbdas)
[<matplotlib.lines.Line2D at 0x128ecd2b0>]
choices = np.random.choice(simu_lbdas.shape[0], 100)
choices
array([268, 202, 67, 203, 274, 321, 161, 283, 105, 414, 196, 32, 96,
313, 45, 438, 173, 377, 358, 108, 301, 178, 143, 377, 374, 276,
120, 497, 57, 489, 461, 152, 223, 103, 487, 184, 361, 271, 234,
224, 344, 175, 429, 199, 193, 295, 273, 23, 430, 122, 107, 483,
47, 440, 152, 342, 289, 21, 195, 375, 8, 469, 164, 393, 344,
408, 69, 319, 423, 495, 223, 105, 277, 329, 225, 334, 227, 119,
303, 294, 196, 376, 147, 293, 117, 467, 307, 313, 234, 469, 238,
266, 116, 13, 221, 148, 116, 345, 164, 256])
plt.plot(simu_lbdas, alpha=0.3)
plt.plot(choices, simu_lbdas[choices], 'o')
[<matplotlib.lines.Line2D at 0x1284498d0>]
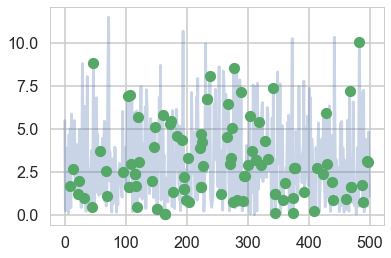
simlamsmall = simu_lbdas[choices]
simysmall = simy[choices,:]
simysmall.shape
(100, 365)
junkm = model_poisson1(4, y.shape[0], observed=simy[53,:])
with junkm:
junkt = pm.sample(3000, tune=1000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:03<00:00, 2529.59draws/s]
simu_lbdas[53]
2.1571347219574495
pm.traceplot(junkt)
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_base.py:3604: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
alternative='`bottom`', obj_type='argument')
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x12c28c438>,
<matplotlib.axes._subplots.AxesSubplot object at 0x128a318d0>]],
dtype=object)

pm.summary(junkt)
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| lambda | 2.186212 | 0.077299 | 0.001335 | 2.040262 | 2.344938 | 2550.350587 | 0.999855 |
junkt.report.ok
True
junkt['lambda'].shape
(6000,)
R=100
sbcpost = np.zeros((R, 6000))
problems = [False]*R
summaries = []
for i in range(R):
m = model_poisson1(4, y.shape[0], observed=simysmall[i,:])
junkt = pm.sample(3000, tune=1000, model=m, progressbar=False)
sbcpost[i,:] = junkt['lambda']
s = pm.stats.summary(junkt,varnames=['lambda'])
summaries.append(s)
problems[i] = junkt.report.ok
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8825518725681838, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8829819214760952, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8797957787550474, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8803631883661142, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8847092815626316, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.8792446343358976, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.881944264363315, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
The acceptance probability does not match the target. It is 0.878943315484823, but should be close to 0.8. Try to increase the number of tuning steps.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
plt.plot(simlamsmall, 'o', alpha=0.3)
plt.plot(np.array(range(R))[problems], simlamsmall[problems], 'o')
[<matplotlib.lines.Line2D at 0x12c436400>]
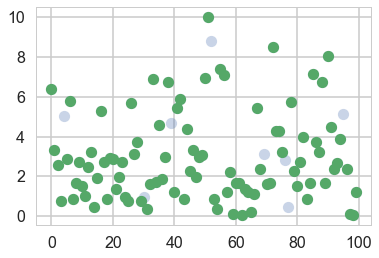
Calculating simulated posterior statistics
def sbc_rank(source_param, param_post, thin):
return np.sum(source_param < param_post[::thin])
def z_scores_func(source_param, param_post):
mean_param = np.mean(param_post)
std_param = np.std(param_post)
zs = np.abs(mean_param - source_param)/std_param
return zs
def shrinkages_func(std_source, param_post):
std_param = np.std(param_post)
zs = 1. - (std_param*std_param)/(std_source*std_source)
return zs
summaries[0]
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| lambda | 6.414486 | 0.130675 | 0.002855 | 6.167806 | 6.670111 | 2382.524697 | 1.000655 |
# posterior sensitivities analysis
z_scores = np.zeros(R)
shrinkages = np.zeros(R)
for i, s in enumerate(summaries):
post_mean_lbda = s['mean'].values[0]
#post_sd_lbda = s['sd'].values[0]
prior_sd_lbda = 4.0
print(simlamsmall[i], post_mean_lbda)
#z_scores[i] = np.abs((post_mean_lbda - simlamsmall[i]) / post_sd_lbda)
z_scores[i] = z_scores_func(simlamsmall[i], sbcpost[i,:])
#shrinkages[i] = 1 - (post_sd_lbda / prior_sd_lbda ) ** 2
shrinkages[i] = shrinkages_func(prior_sd_lbda, sbcpost[i,:])
6.41723985519039 6.414485564553586
3.3375481460770304 3.1903701333540133
2.566627451857849 2.543248872319566
0.7465858830269789 0.715877420202882
5.0515144524177895 4.975233023669956
2.8790333587143393 2.9148706558430275
5.789695782063364 5.824930845003097
0.8526796954786386 0.835003235467652
1.6579202801044672 1.6732910589120487
2.744400581569949 2.8095663942992086
1.5002597776031485 1.5680736515805316
1.0051570244822148 0.9779972012691904
2.4921784512697176 2.4606009069430086
3.210259909361477 3.109322040123031
0.4572400711835704 0.46030298909603257
1.9237431849458069 1.8465502032584742
5.291027482053392 5.240691518515105
2.744550074199637 2.771484627057473
0.8499338566006396 0.895314876548667
2.9405893841905266 3.059250819354544
2.88990476422701 2.8917614128496605
1.3500860565448067 1.3592211878100222
1.9750124952368815 1.8863896368281603
2.744550074199637 2.7734548689864473
0.9693189019739621 1.0056656397713153
0.774101496493859 0.7096863357577977
5.668384942053783 5.539701574489197
3.1036126384557 3.0281361648425613
3.745756478216811 3.5879929394683887
0.7676112007009431 0.7761477642744253
0.9367821045502362 0.8117141913653386
0.36711139752110356 0.3409599996599431
1.6240545053976507 1.602277035759763
6.880336284409727 6.945146451480416
1.7266279410660093 1.6940741911008492
4.592310576749811 4.628558916285208
1.8569438977055963 1.7887883524259771
2.97490022285298 2.864618449232959
6.734393541803753 6.774427297271684
4.708152649298847 4.882530816730709
1.2285187015654833 1.2203128400012895
5.454181432638862 5.514396483693017
5.90380400267185 5.706415568228287
0.8816579795618298 0.8638589711919344
4.38295840893627 4.460872402223795
2.25252318389187 2.3558201000518038
3.333332282265827 3.2091317357281084
1.9806000890144357 2.129168450275471
2.9687517855293395 2.8982693794429615
3.0807347983198587 3.074932933898502
6.967620323534478 6.955807716202042
10.017564482457619 10.225275528589028
8.821440037923772 8.600600312083166
0.8516367802302435 0.8253529229933483
0.36711139752110356 0.34227949351518716
7.384021865554807 7.320817178542294
7.1202353546587025 7.471007631871554
1.212181179040889 1.2102371208731166
2.236689855148519 2.2438458901147356
0.11111482644811253 0.12413708666853136
1.672294919372901 1.5522137657274895
1.6397712692170883 1.639597187404476
0.0683657109362711 0.0684443893185653
1.3505752432044167 1.3865067965585514
1.2285187015654833 1.2171922075344765
0.21789862513285682 0.17010448721879884
1.0946235127073893 1.1620255167355107
5.423964630904606 5.568574450966693
2.355271800070208 2.343124253052943
3.142378352140631 3.284832522326769
1.6240545053976507 1.6006868748486331
1.6579202801044672 1.6740358584212294
8.50209722588145 8.278164191865518
4.300661652744093 4.402597015996311
4.2605728901311775 3.9659144801139767
3.2349221852795766 3.237188511946372
2.8279695371929705 2.9471877346647775
0.45916031837062726 0.43147391839518334
5.759413143859845 5.686997183779262
2.2547623896661735 2.427701660710945
1.5002597776031485 1.5681066683421547
2.73124484754489 2.5479704737049644
3.9721430367121697 3.7981634469028602
0.8394580527286565 0.7847808473533251
1.6892653177536772 1.7809666574562946
7.175380822644326 7.17359231408961
3.739629870575026 3.768000042134631
3.210259909361477 3.107242474635106
6.734393541803753 6.772289642665042
1.6397712692170883 1.6425287965976871
8.049301155717458 8.18385840021637
4.507356626853358 4.468423460985501
2.3556843774074094 2.4132529307053656
2.6662507006004685 2.660512696387857
3.901350955248992 4.116156895086786
5.133374656183931 5.456219518652679
2.3556843774074094 2.4136491261905855
0.09671933230949659 0.09113862599257729
0.0683657109362711 0.06853832668227812
1.2218014645416215 1.1801929045610626
Shrinkage Plot
plt.plot(shrinkages, z_scores, '.');
plt.xlim([0,1]);
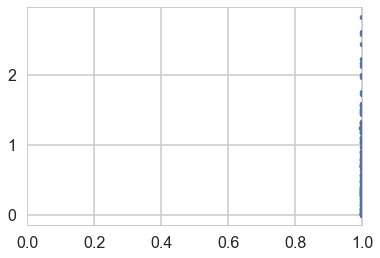
Simulation Based Callibration
ranks=np.empty(R, dtype='int')
for i, lam in enumerate(simlamsmall):
ranks[i] = sbc_rank(lam, sbcpost[i,:], 4)
ranks
array([ 730, 95, 556, 384, 366, 969, 903, 517, 882, 1158, 1255,
445, 535, 214, 794, 206, 520, 900, 1242, 1355, 753, 816,
177, 927, 1158, 110, 210, 301, 88, 855, 8, 294, 549,
1038, 437, 924, 244, 152, 911, 1409, 647, 1020, 90, 554,
1132, 1342, 163, 1462, 328, 678, 690, 1345, 114, 422, 302,
474, 1490, 718, 802, 1121, 68, 744, 715, 1059, 631, 21,
1323, 1321, 634, 1398, 549, 884, 124, 1245, 3, 760, 1362,
326, 442, 1476, 1287, 21, 70, 179, 1364, 759, 935, 200,
915, 785, 1228, 540, 1119, 722, 1461, 1498, 1158, 515, 740,
313])
# 1500 left over samples after thinning, 1501 spots, 100 replications
sbc_low = stats.binom.ppf(0.005, R, 150.0 / 1500)
sbc_mid = stats.binom.ppf(0.5, R, 150.0 / 1500)
sbc_high = stats.binom.ppf(0.995, R, 150.0 / 1500)
plt.hist(ranks, bins=[150*x for x in range(11)]);
plt.axhline(sbc_low, 0,1, c='r')
plt.axhline(sbc_mid, 0,1, c='r')
plt.axhline(sbc_high, 0,1, c='r')
<matplotlib.lines.Line2D at 0x128daa908>
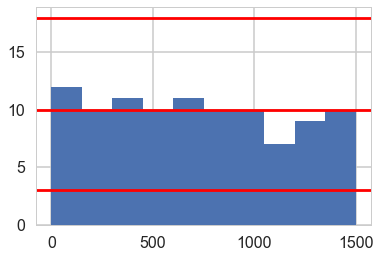
Posterior Predictive Check
mpo = model_poisson1(4, y.shape[0], observed=y)
with mpo:
samples = pm.sample(3000, tune=1000)
posterior = samples.get_values('lambda')
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:03<00:00, 2598.48draws/s]
pm.traceplot(samples)
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_base.py:3604: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
alternative='`bottom`', obj_type='argument')
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x12eb4feb8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x12cb30908>]],
dtype=object)

with mpo:
samples_ppc = pm.sample_ppc(samples)
100%|██████████| 3000/3000 [00:01<00:00, 2636.15it/s]
samples_ppc['obsv'].shape
(3000, 365)
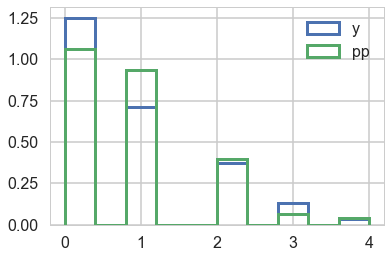
plt.hist(y, normed=True, histtype='step', lw=3, label="y");
plt.hist(samples_ppc['obsv'][0,:], normed=True, histtype='step', lw=3, label="pp")
plt.legend();
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_axes.py:6521: MatplotlibDeprecationWarning:
The 'normed' kwarg was deprecated in Matplotlib 2.1 and will be removed in 3.1. Use 'density' instead.
alternative="'density'", removal="3.1")
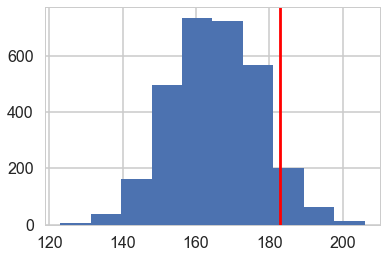
zeros = np.zeros(3000)
for i in range(3000):
zeros[i] = np.sum(samples_ppc['obsv'][i,:]==0)
plt.hist(zeros)
plt.axvline(np.sum(y==0), 0,1, c='r')
<matplotlib.lines.Line2D at 0x12edc9438>
A second model: 0 inflated poisson
The likelihood that combines the two cases considered above is called the Zero Inflated poisson. It has two arguments, the Poisson rate parameter, and the proportion of poisson variates (theta and psi in pymc).
def model_0ipoisson1(sd, shp, observed=None):
with pm.Model() as model:
lam=pm.HalfNormal("lambda", sd)
theta=pm.Beta("theta", 1,1)
like = pm.ZeroInflatedPoisson("obsv", theta=lam, psi=theta, shape = shp, observed=observed)
return model
model2 = model_0ipoisson1(4, y.shape[0], observed=y)
with model2:
trace2 = pm.sample(3000, tune=1000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1223.84draws/s]
pm.traceplot(trace2);
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_base.py:3604: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
alternative='`bottom`', obj_type='argument')
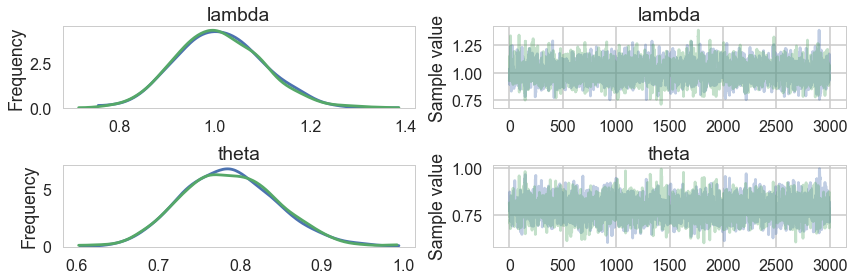
pm.summary(trace2)
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| lambda | 1.010743 | 0.090270 | 0.001997 | 0.841846 | 1.188071 | 1877.185581 | 0.999891 |
| theta | 0.787184 | 0.058392 | 0.001319 | 0.673310 | 0.897211 | 1842.570275 | 0.999837 |
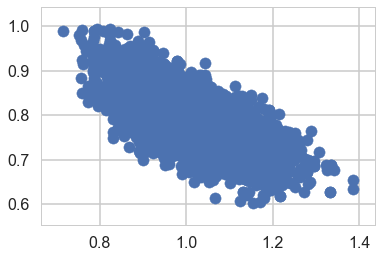
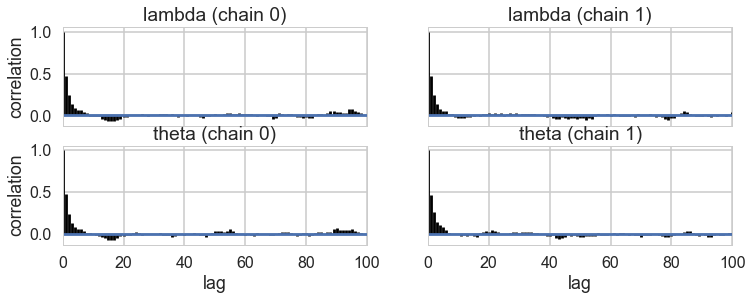
Identifiability Problems through simple prior-predictive checks
plt.scatter(trace2['lambda'], trace2['theta'])
<matplotlib.collections.PathCollection at 0x130961208>
pm.autocorrplot(trace2)
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x130cd0a20>,
<matplotlib.axes._subplots.AxesSubplot object at 0x130cc6f60>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x130d042e8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x130dc8668>]],
dtype=object)
Sampling some prior predictives
We sample those likely to be troublesome, especially high drunkenness probability, and low productivity
simu_lbdas2 = stats.halfnorm(scale=4).rvs(500)
simu_betas2 = stats.beta(1,1).rvs(500)
simy2 = np.zeros((500, N))
for i in range(500):
simu_bern = stats.bernoulli(1 - simu_betas2[i]).rvs(N).astype('bool')
indices = np.array(range(N))[simu_bern]
simy2[i,indices] = stats.poisson(simu_lbdas2[i]).rvs(indices.shape[0])
simy2[0,:].shape, simy2[53,:].shape
((365,), (365,))
lowlamindices = np.argsort(simu_lbdas2)[:5]
lowlamindices, simu_lbdas2[lowlamindices]
(array([211, 149, 489, 61, 235]),
array([8.21614304e-05, 2.67515303e-03, 3.93248405e-03, 4.44471181e-03,
5.28773436e-03]))
highpindices = np.argsort(simu_betas2)[-5:]
highpindices, simu_betas2[highpindices]
(array([290, 65, 231, 487, 263]),
array([0.98278988, 0.98723031, 0.99244229, 0.99354593, 0.99973682]))
reps_to_sample = np.concatenate((lowlamindices, highpindices))
reps_to_sample
array([211, 149, 489, 61, 235, 290, 65, 231, 487, 263])
reps_to_sample2 = np.concatenate((np.argsort(simu_lbdas2)[181:186], np.argsort(simu_betas2)[181:186]))
for j in reps_to_sample:
m = model_0ipoisson1(4, N, observed=simy2[j,:])
t = pm.sample(3000, tune=1000, model=m)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:07<00:00, 1056.93draws/s]
There were 6 divergences after tuning. Increase `target_accept` or reparameterize.
There were 27 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:07<00:00, 1088.21draws/s]
There were 13 divergences after tuning. Increase `target_accept` or reparameterize.
There were 17 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:08<00:00, 911.35draws/s]
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:07<00:00, 1076.51draws/s]
There were 12 divergences after tuning. Increase `target_accept` or reparameterize.
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:08<00:00, 912.17draws/s]
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1602.74draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1446.49draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:07<00:00, 1002.20draws/s]
There were 7 divergences after tuning. Increase `target_accept` or reparameterize.
There were 19 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:08<00:00, 948.62draws/s]
There were 10 divergences after tuning. Increase `target_accept` or reparameterize.
There were 12 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:08<00:00, 942.51draws/s]
There were 8 divergences after tuning. Increase `target_accept` or reparameterize.
There were 8 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.
for j in reps_to_sample2:
m = model_0ipoisson1(4, N, observed=simy2[j,:])
t = pm.sample(3000, tune=1000, model=m)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1701.98draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1507.52draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1425.50draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1623.30draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1268.53draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1260.10draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1585.96draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:07<00:00, 1091.63draws/s]
The number of effective samples is smaller than 25% for some parameters.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1612.43draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1609.68draws/s]
In search of a better model
Lets throw in some domain expertise
A survey of Abbey Heads has told us, that the most a monk would produce, even at low productivity, one manuscript a day.
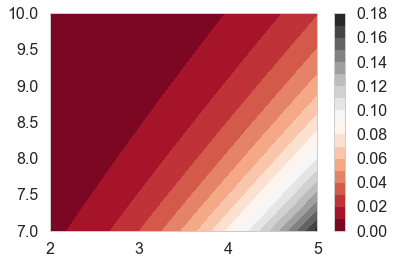
Choosing better Priors
cdfig = lambda alpha, beta: stats.invgamma(alpha,scale=beta).cdf(1)
asp = np.linspace(2,5,100)
bsp = np.linspace(7,10,100)
aa,bb = np.meshgrid(asp, bsp)
aa
array([[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ],
[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ],
[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ],
...,
[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ],
[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ],
[2. , 2.03030303, 2.06060606, ..., 4.93939394, 4.96969697,
5. ]])
z=cdfig(aa,bb)
plt.contourf(aa, bb, z, 20, cmap='RdGy')
plt.colorbar();
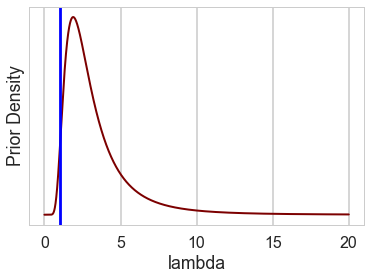
lbda = np.linspace(0, 20, num=int(20/0.001))
alpha=3.5
beta=8.5
pdf = stats.invgamma(alpha, scale=beta)
plt.plot(lbda, pdf.pdf(lbda), c=c_dark_highlight, lw=2)
plt.xlabel("lambda"); plt.ylabel("Prior Density"); plt.yticks([]);
plt.axvline(1, 0, 1, c="blue")
<matplotlib.lines.Line2D at 0x12ded14e0>
stats.invgamma(alpha, scale=beta).cdf(1.), 1 - stats.invgamma(alpha, scale=beta).cdf(9.)
(0.017396182569124504, 0.0342667918309546)
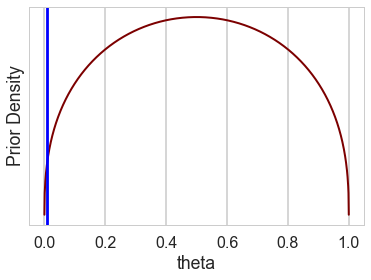
theta = np.linspace(0, 1, num=int(1/0.001))
curve=1.4
pdf = stats.beta(curve, curve)
plt.plot(theta, pdf.pdf(theta), c=c_dark_highlight, lw=2)
plt.xlabel("theta"); plt.ylabel("Prior Density"); plt.yticks([]);
plt.axvline(0.01, 0, 1, c="blue")
<matplotlib.lines.Line2D at 0x131fb55f8>
stats.beta(curve, curve).cdf(0.2), 1 - stats.beta(curve, curve).cdf(0.8)
(0.15200913356356724, 0.15200913356356716)
def model_0ipoisson2(alpha, beta, curve, shp, observed=None):
with pm.Model() as model:
lam = pm.InverseGamma("lambda",alpha=alpha,beta=beta)
theta=pm.Beta("theta", curve, curve)
like = pm.ZeroInflatedPoisson("obsv", theta=lam, psi=theta, shape = shp, observed=observed)
return model
Quick Posterior Predictive
We will in a later notebook, do the whole workflow, but in the meanwhile, here is the posterior predictive
model3 = model_0ipoisson2(alpha, beta, curve, y.shape[0], observed=y)
with model3:
trace3 = pm.sample(3000, tune=1000)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1263.90draws/s]
pm.summary(trace3)
| mean | sd | mc_error | hpd_2.5 | hpd_97.5 | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|
| lambda | 1.047114 | 0.091194 | 0.001884 | 0.865752 | 1.219998 | 2129.650694 | 0.999833 |
| theta | 0.769899 | 0.056432 | 0.001331 | 0.661380 | 0.879076 | 1779.443335 | 1.000031 |
pm.traceplot(trace3)
//anaconda/envs/py3l/lib/python3.6/site-packages/matplotlib/axes/_base.py:3604: MatplotlibDeprecationWarning:
The `ymin` argument was deprecated in Matplotlib 3.0 and will be removed in 3.2. Use `bottom` instead.
alternative='`bottom`', obj_type='argument')
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x12e56ab38>,
<matplotlib.axes._subplots.AxesSubplot object at 0x12e3f1be0>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x12efab9e8>,
<matplotlib.axes._subplots.AxesSubplot object at 0x132289fd0>]],
dtype=object)
Sampling some prior predictives
Once again, we are looking at those likely to be troublesome…
simu_lbdas3 = stats.invgamma(alpha, scale=beta).rvs(500)
simu_betas3 = stats.beta(curve, curve).rvs(500)
simy3 = np.zeros((500, N))
for i in range(500):
simu_bern = stats.bernoulli(1 - simu_betas3[i]).rvs(N).astype('bool')
indices = np.array(range(N))[simu_bern]
simy3[i,indices] = stats.poisson(simu_lbdas3[i]).rvs(indices.shape[0])
lowlamindices = np.argsort(simu_lbdas2)[:5]
lowlamindices, simu_lbdas2[lowlamindices]
(array([211, 149, 489, 61, 235]),
array([8.21614304e-05, 2.67515303e-03, 3.93248405e-03, 4.44471181e-03,
5.28773436e-03]))
for j in lowlamindices:
m = model_0ipoisson2(alpha, beta, curve, N, observed=simy2[j,:])
t = pm.sample(3000, tune=1000, model=m)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1541.88draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1659.39draws/s]
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1522.45draws/s]
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1413.76draws/s]
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1468.52draws/s]
highpindices = np.argsort(simu_betas2)[-5:]
highpindices, simu_betas2[highpindices]
(array([316, 399, 138, 437, 281]),
array([0.99376565, 0.99656648, 0.99745191, 0.99795533, 0.99821804]))
for j in highpindices:
m = model_0ipoisson2(alpha, beta, curve, N, observed=simy2[j,:])
t = pm.sample(3000, tune=1000, model=m)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1564.07draws/s]
There was 1 divergence after tuning. Increase `target_accept` or reparameterize.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:04<00:00, 1696.81draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1324.69draws/s]
There were 5 divergences after tuning. Increase `target_accept` or reparameterize.
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:06<00:00, 1282.83draws/s]
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (2 chains in 2 jobs)
NUTS: [theta, lambda]
Sampling 2 chains: 100%|██████████| 8000/8000 [00:05<00:00, 1561.93draws/s]