Keywords: gradient descent |  logistic regression |  pytorch |  sgd |  minibatch sgd |  Data: iris_dataset.pickle |  Download Notebook

Contents

Contents

Learning Aims

Lab Trajectory

Installing PyTorch

Installation

OS X/Linux

We shall be using PyTorch in this class. Please go to the PyTorch website where they have a nicely designed interface for installation instructions depending on your OS (Linux/OS X), your package management system (pip/conda) and your CUDA install (8/9/none). http://pytorch.org. Your installation instructions will look something like:

or

Windows

PyTorch doesn’t have official Windows support as yet, but there are Windows binaries available due to Github user @peter123. Please see his PyTorch for Windows repo https://github.com/peterjc123/pytorch-scripts for installation instructions for different versions of Windows and CUDA. In all likelihood your installation instructions will be:

Testing Installation

If the code cell shows an error, then your PyTorch installation is not working and you should contact one of the teaching staff.

### Code Cell to Test PyTorch

import torch
print(torch.__version__)
import torchvision
import torchvision.transforms as transforms
print(torchvision.__version__)

x = torch.rand(5, 3)
print(x)

transforms.RandomRotation(0.7)
transforms.RandomRotation([0.9, 0.2])

t = transforms.RandomRotation(10)
angle = t.get_params(t.degrees)

print(angle)


0.3.0.post4
0.2.0

 0.2901  0.8863  0.4383
 0.9738  0.9825  0.1046
 0.8069  0.1135  0.3565
 0.4906  0.4698  0.9623
 0.1116  0.4729  0.3536
[torch.FloatTensor of size 5x3]

-8.447796634522254

Why PyTorch?

All the quotes will come from the PyTorch About Page http://pytorch.org/about/ from which I’ll plagiarize shamelessly. After all, who better to tout the virtues of PyTorch than the creators?

What is PyTorch?

According to the PyTorch about page, “PyTorch is a python package that provides two high-level features:

It’s quite fast

“PyTorch has minimal framework overhead. We integrate acceleration libraries such as Intel MKL and NVIDIA (CuDNN, NCCL) to maximize speed. At the core, it’s CPU and GPU Tensor and Neural Network backends (TH, THC, THNN, THCUNN) are written as independent libraries with a C99 API. They are mature and have been tested for years.

Hence, PyTorch is quite fast – whether you run small or large neural networks.”

Imperative programming experience

“PyTorch is designed to be intuitive, linear in thought and easy to use. When you execute a line of code, it gets executed. There isn’t an asynchronous view of the world. When you drop into a debugger, or receive error messages and stack traces, understanding them is straight-forward. The stack-trace points to exactly where your code was defined. We hope you never spend hours debugging your code because of bad stack traces or asynchronous and opaque execution engines.”

“PyTorch is not a Python binding into a monolothic C++ framework. It is built to be deeply integrated into Python. You can use it naturally like you would use numpy / scipy / scikit-learn etc. You can write your new neural network layers in Python itself, using your favorite libraries and use packages such as Cython and Numba. Our goal is to not reinvent the wheel where appropriate.”

Takes advantage of GPUs easily

“PyTorch provides Tensors that can live either on the CPU or the GPU, and accelerate compute by a huge amount.

We provide a wide variety of tensor routines to accelerate and fit your scientific computation needs such as slicing, indexing, math operations, linear algebra, reductions. And they are fast!”

Dynamic Graphs!!!

“Most frameworks such as TensorFlow, Theano, Caffe and CNTK have a static view of the world. One has to build a neural network, and reuse the same structure again and again. Changing the way the network behaves means that one has to start from scratch.

With PyTorch, we use a technique called Reverse-mode auto-differentiation, which allows you to change the way your network behaves arbitrarily with zero lag or overhead. Our inspiration comes from several research papers on this topic, as well as current and past work such as autograd, autograd, Chainer, etc.

While this technique is not unique to PyTorch, it’s one of the fastest implementations of it to date. You get the best of speed and flexibility for your crazy research.”

Working with PyTorch Basics

Enough of the sales pitch! Let’s start to understand the PyTorch basics.

The basic unit of PyTorch is a tensor (basically a multi-dimensional array like a np.ndarray).

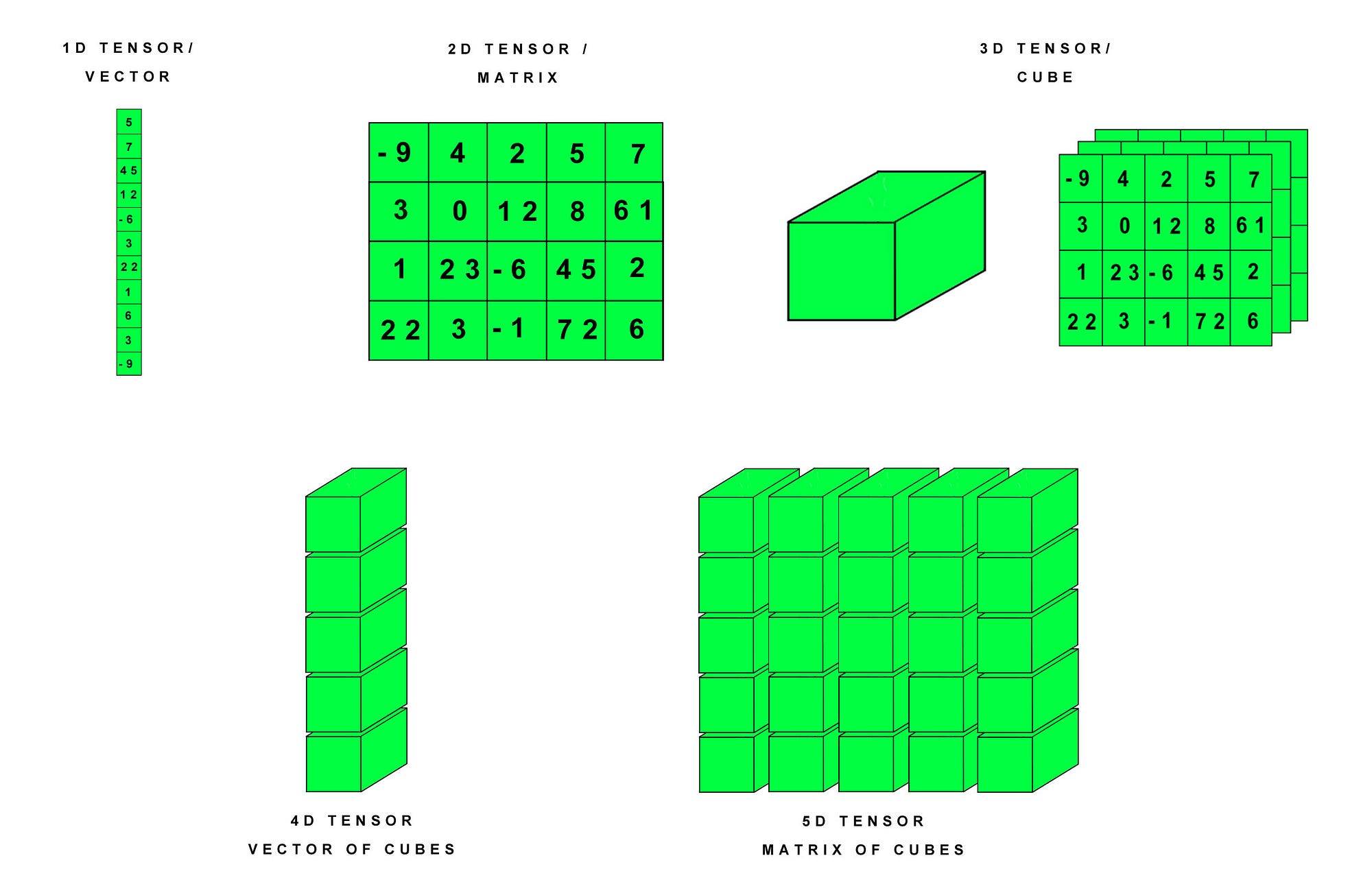
(image borrowed from https://hackernoon.com/learning-ai-if-you-suck-at-math-p4-tensors-illustrated-with-cats-27f0002c9b32 )

We can create PyTorch tensors directly.


## You can create torch.Tensor objects by giving them data directly

#  1D vector
vector_input = [1., 2., 3., 4., 5., 6.]
vector = torch.Tensor(vector_input)

# Matrix
matrix_input = [[1., 2., 3.], [4., 5., 6]]
matrix = torch.Tensor(matrix_input)

# Create a 3D tensor of size 2x2x2.
tensor_input = [[[1., 2.], [3., 4.]],
          [[5., 6.], [7., 8.]]]
tensor3d = torch.Tensor(tensor_input)


print(vector)
print(matrix)
print(tensor3d)

 1
 2
 3
 4
 5
 6
[torch.FloatTensor of size 6]


 1  2  3
 4  5  6
[torch.FloatTensor of size 2x3]


(0 ,.,.) = 
  1  2
  3  4

(1 ,.,.) = 
  5  6
  7  8
[torch.FloatTensor of size 2x2x2]

They can be created without any initialization or initialized with random data from uniform (rand()) or normal (randn()) distributions

# Tensors with no initialization
x_1 = torch.Tensor(2, 5)
y_1 = torch.Tensor(3, 5)
print(x_1)
print(y_1)

# Tensors initialized from uniform
x_2 = torch.rand(5, 3)
y_2 = torch.rand(5, 5)

print(x_2)
print(y_2)

# Tensors initialized from normal
x_3 = torch.randn(5, 3)
y_3 = torch.randn(5, 5)

print(x_3)
print(y_3)

 0.0000e+00  1.0842e-19  6.3095e+27  1.0845e-19  1.8217e-44
 0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
[torch.FloatTensor of size 2x5]


 0.0000e+00  1.0842e-19  0.0000e+00  1.0842e-19  5.6052e-45
 0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00  1.0842e-19
 6.3059e+27 -1.5849e+29  2.8026e-45  1.0842e-19  4.9077e+27
[torch.FloatTensor of size 3x5]


 0.5759  0.0052  0.5583
 0.6048  0.9838  0.5592
 0.9206  0.8251  0.5032
 0.5607  0.0485  0.4050
 0.6590  0.7941  0.6106
[torch.FloatTensor of size 5x3]


 0.0325  0.7753  0.2360  0.6659  0.7960
 0.1888  0.4185  0.9106  0.8155  0.1502
 0.6387  0.9303  0.7255  0.1813  0.5066
 0.9799  0.9844  0.2526  0.0286  0.1560
 0.8586  0.2915  0.5509  0.5185  0.5027
[torch.FloatTensor of size 5x5]


-1.7841 -0.1001 -0.6045
 0.1409  0.6862  0.8469
 0.8223  2.1229 -0.2956
 0.6558 -1.1188 -0.2326
 1.2631  0.2665 -0.0208
[torch.FloatTensor of size 5x3]


-0.0194 -2.0925  0.9395 -0.0195  1.3913
 1.9729  0.5524 -1.0353 -0.0404 -0.4854
-0.3671 -0.1941 -0.6049 -1.7765  0.2992
 0.1015 -1.2305 -1.1176  0.0383  1.0059
-1.6558 -0.9154 -0.6085 -0.9777  0.8537
[torch.FloatTensor of size 5x5]

The expected operations (arithmetic operations, addressing, etc) are all in place.

# Expect (2,5)
x_1.size()

print(x_1)


# Addition
print(x_2)
print(x_3)

print(x_2+ x_3)

# Addressing
print(x_3[:, 2])

 0.0000e+00  1.0842e-19  6.3095e+27  1.0845e-19  1.8217e-44
 0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
[torch.FloatTensor of size 2x5]


 0.5759  0.0052  0.5583
 0.6048  0.9838  0.5592
 0.9206  0.8251  0.5032
 0.5607  0.0485  0.4050
 0.6590  0.7941  0.6106
[torch.FloatTensor of size 5x3]


-1.7841 -0.1001 -0.6045
 0.1409  0.6862  0.8469
 0.8223  2.1229 -0.2956
 0.6558 -1.1188 -0.2326
 1.2631  0.2665 -0.0208
[torch.FloatTensor of size 5x3]


-1.2081 -0.0949 -0.0462
 0.7457  1.6700  1.4062
 1.7429  2.9480  0.2075
 1.2165 -1.0703  0.1724
 1.9221  1.0606  0.5898
[torch.FloatTensor of size 5x3]


-0.6045
 0.8469
-0.2956
-0.2326
-0.0208
[torch.FloatTensor of size 5]

It’s easy to move between PyTorch and Numpy worlds with numpy() and torch.from_numpy()

# PyTorch --> Numpy
print(x_1)
print(x_1.numpy())

print(type(x_1))
print(type(x_1.numpy()))

numpy_x_1 = x_1.numpy()
pytorch_x_1 = torch.from_numpy(numpy_x_1)

print(type(numpy_x_1))
print(type(pytorch_x_1))

 0.0000e+00  1.0842e-19  6.3095e+27  1.0845e-19  1.8217e-44
 0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
[torch.FloatTensor of size 2x5]

[[  0.00000000e+00   1.08420217e-19   6.30950545e+27   1.08446661e-19
    1.82168800e-44]
 [  0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00
    0.00000000e+00]]
<class 'torch.FloatTensor'>
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
<class 'torch.FloatTensor'>

Finally PyTorch provides some convenience mechanisms for concatenating Tensors via torch.cat() and reshaping them with .view()

## Concatenating

# By default, it concatenates along the first axis (concatenates rows)
x_1 = torch.randn(2, 5)
y_1 = torch.randn(3, 5)
z_1 = torch.cat([x_1, y_1])
print(z_1)

# Concatenate columns:
x_2 = torch.randn(2, 3)
y_2 = torch.randn(2, 5)
# second arg specifies which axis to concat along
z_2 = torch.cat([x_2, y_2], 1)
print(z_2)

## Reshaping
x = torch.randn(2, 3, 4)
print(x)
print(x.view(2, 12))  # Reshape to 2 rows, 12 columns
# Same as above.  If one of the dimensions is -1, its size can be inferred
print(x.view(2, -1))

 0.0000e+00  1.0842e-19  6.3095e+27  1.0845e-19  1.8217e-44
 0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00  0.0000e+00
[torch.FloatTensor of size 2x5]

[[  0.00000000e+00   1.08420217e-19   6.30950545e+27   1.08446661e-19
    1.82168800e-44]
 [  0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00
    0.00000000e+00]]
<class 'torch.FloatTensor'>
<class 'numpy.ndarray'>
<class 'numpy.ndarray'>
<class 'torch.FloatTensor'>

Ok – in order to understand variables in PyTorch, let’s take a break and learn about Artificial Neural Networks.

PyTorch Variables and the Computational Graph

Ok – back to PyTorch.

The other fundamental PyTorch construct besides Tensors are Variables. Variables are very similar to tensors, but they also keep track of the graph (including their gradients for autodifferentiation). They are defined in the autograd module of torch.

from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

# Let's create a variable by initializing it with a tensor
first_tensor = torch.Tensor([23.3])

first_variable = Variable(first_tensor, requires_grad=True)

print("first variables gradient: ", first_variable.grad)
print("first variables data: ", first_variable.data)



first variables gradient:  None
first variables data:  
 23.3000
[torch.FloatTensor of size 1]

Now let’s create some new variables. We can do so implicitly just by creating other variables with functional relationships to our variable.

x = first_variable
y = (x ** x) * (x - 2) # y is a variable
z = F.tanh(y) # z has a functional relationship to y, it's a variable
z.backward()

print("y.data: ", y.data)
print("y.grad: ", y.grad)

print("z.data: ", z.data)
print("z.grad: ", z.grad)

print("x.grad:", x.grad)



y.data:  
 1.5409e+33
[torch.FloatTensor of size 1]

y.grad:  None
z.data:  
 1
[torch.FloatTensor of size 1]

z.grad:  None
x.grad: Variable containing:
 0
[torch.FloatTensor of size 1]

Variables come with a .backward() that allows them to do autodifferentiation via backwards propagation.

Constructing a model with PyTorch

Constructing a model with PyTorch is based on a design pattern with a fairly repeatable three step process:

from sklearn.datasets import make_regression
import numpy as np
np.random.seed(99)
x1_data, y1_data, coef = make_regression(30,10, 10, bias=1, noise=2, coef=True)

x1_data = [x1_data[i:i+1] for i in range(0, len(x1_data), 1)]
y1_data = [y1_data[i:i+1] for i in range(0, len(y1_data), 1)]

import torch
from torch.autograd import Variable

x_data = Variable(torch.Tensor(x1_data))
y_data = Variable(torch.Tensor(y1_data))


class Model(torch.nn.Module):

    def __init__(self):
        """
        In the constructor we instantiate two nn.Linear module
        """
        super(Model, self).__init__()
        self.linear = torch.nn.Linear(10, 1)  # One in and one out

    def forward(self, x):
        """
        In the forward function we accept a Variable of input data and we must return
        a Variable of output data. We can use Modules defined in the constructor as
        well as arbitrary operators on Variables.
        """
        y_pred = self.linear(x)
        return y_pred

# our model
model = Model()


# Construct our loss function and an Optimizer. The call to model.parameters()
# in the SGD constructor will contain the learnable parameters of the two
# nn.Linear modules which are members of the model.
criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

# Training loop
for epoch in range(500):
    
    # Forward pass: Compute predicted y by passing x to the model
    y_pred = model(x_data)

    # Compute and print loss
    loss = criterion(y_pred, y_data)
    print(epoch, loss.data[0])

    # Zero gradients, perform a backward pass, and update the weights.
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()


# After training
ytrain_pred = model(x_)


0 726254.125
1 124822.0
2 54632.37890625
3 28299.19921875
4 15898.6708984375
5 9425.998046875
6 5830.21484375
7 3738.6923828125
8 2474.47607421875
9 1683.9019775390625
10 1174.31640625
11 837.0162353515625
12 608.6522827148438
13 451.1288757324219
14 340.83050537109375
15 262.689208984375
16 206.82933044433594
17 166.6243896484375
18 137.53953552246094
19 116.42092895507812
20 101.04288482666016
21 89.822998046875
22 81.62397003173828
23 75.62706756591797
24 71.23649597167969
25 68.02033996582031
26 65.66402435302734
27 63.936065673828125
28 62.66962432861328
29 61.74079132080078
30 61.05937957763672
31 60.55976867675781
32 60.1931037902832
33 59.92445373535156
34 59.7275505065918
35 59.5826301574707
36 59.47638702392578
37 59.39829635620117
38 59.341041564941406
39 59.29940414428711
40 59.26884078979492
41 59.24623107910156
42 59.229835510253906
43 59.21748733520508
44 59.208683013916016
45 59.20254898071289
46 59.197391510009766
47 59.19389724731445
48 59.19124984741211
49 59.18930435180664
50 59.1878662109375
51 59.186649322509766
52 59.18614959716797
53 59.1855583190918
54 59.185325622558594
55 59.185020446777344
56 59.18451690673828
57 59.18470001220703
58 59.18440628051758
59 59.18421936035156
60 59.184173583984375
61 59.184513092041016
62 59.18410110473633
63 59.184043884277344
64 59.18428421020508
65 59.18429183959961
66 59.18418884277344
67 59.184200286865234
68 59.18415832519531
69 59.184078216552734
70 59.18434143066406
71 59.18395233154297
72 59.184078216552734
73 59.18425369262695
74 59.18419647216797
75 59.18400192260742
76 59.18406295776367
77 59.18445587158203
78 59.183876037597656
79 59.18396759033203
80 59.184043884277344
81 59.18427658081055
82 59.1843376159668
83 59.18402099609375
84 59.18409729003906
85 59.18416976928711
86 59.184112548828125
87 59.18427276611328
88 59.184295654296875
89 59.184444427490234
90 59.18429183959961
91 59.184329986572266
92 59.184513092041016
93 59.18413162231445
94 59.18425369262695
95 59.18431854248047
96 59.18419647216797
97 59.184288024902344
98 59.184173583984375
99 59.184226989746094
100 59.18417739868164
101 59.18421936035156
102 59.18415832519531
103 59.1842041015625
104 59.18415451049805
105 59.1842041015625
106 59.18415832519531
107 59.184207916259766
108 59.184173583984375
109 59.184207916259766
110 59.18415451049805
111 59.184200286865234
112 59.18414306640625
113 59.184226989746094
114 59.184146881103516
115 59.184226989746094
116 59.18418502807617
117 59.18434524536133
118 59.18442153930664
119 59.18431854248047
120 59.184322357177734
121 59.184295654296875
122 59.18415069580078
123 59.18414306640625
124 59.18423843383789
125 59.184165954589844
126 59.18419647216797
127 59.18421173095703
128 59.184226989746094
129 59.18421936035156
130 59.18425750732422
131 59.184226989746094
132 59.184242248535156
133 59.18424987792969
134 59.184234619140625
135 59.18421936035156
136 59.18425750732422
137 59.184226989746094
138 59.184242248535156
139 59.18424987792969
140 59.184234619140625
141 59.18421936035156
142 59.18425750732422
143 59.184226989746094
144 59.184242248535156
145 59.18424987792969
146 59.184234619140625
147 59.18421936035156
148 59.18425750732422
149 59.184226989746094
150 59.184242248535156
151 59.18424987792969
152 59.184234619140625
153 59.18421936035156
154 59.18425750732422
155 59.184226989746094
156 59.184242248535156
157 59.18424987792969
158 59.184234619140625
159 59.18421936035156
160 59.18425750732422
161 59.184226989746094
162 59.184242248535156
163 59.18424987792969
164 59.184234619140625
165 59.18421936035156
166 59.18425750732422
167 59.184226989746094
168 59.184242248535156
169 59.18424987792969
170 59.184234619140625
171 59.18421936035156
172 59.18425750732422
173 59.184226989746094
174 59.184242248535156
175 59.18424987792969
176 59.184234619140625
177 59.18421936035156
178 59.18425750732422
179 59.184226989746094
180 59.184242248535156
181 59.18424987792969
182 59.184234619140625
183 59.18421936035156
184 59.18425750732422
185 59.184226989746094
186 59.184242248535156
187 59.18424987792969
188 59.184234619140625
189 59.18421936035156
190 59.18425750732422
191 59.184226989746094
192 59.184242248535156
193 59.18424987792969
194 59.184234619140625
195 59.18421936035156
196 59.18425750732422
197 59.184226989746094
198 59.184242248535156
199 59.18424987792969
200 59.184234619140625
201 59.18421936035156
202 59.18425750732422
203 59.184226989746094
204 59.184242248535156
205 59.18424987792969
206 59.184234619140625
207 59.18421936035156
208 59.18425750732422
209 59.184226989746094
210 59.184242248535156
211 59.18424987792969
212 59.184234619140625
213 59.18421936035156
214 59.18425750732422
215 59.184226989746094
216 59.184242248535156
217 59.18424987792969
218 59.184234619140625
219 59.18421936035156
220 59.18425750732422
221 59.184226989746094
222 59.184242248535156
223 59.18424987792969
224 59.184234619140625
225 59.18421936035156
226 59.18425750732422
227 59.184226989746094
228 59.184242248535156
229 59.18424987792969
230 59.184234619140625
231 59.18421936035156
232 59.18425750732422
233 59.184226989746094
234 59.184242248535156
235 59.18424987792969
236 59.184234619140625
237 59.18421936035156
238 59.18425750732422
239 59.184226989746094
240 59.184242248535156
241 59.18424987792969
242 59.184234619140625
243 59.18421936035156
244 59.18425750732422
245 59.184226989746094
246 59.184242248535156
247 59.18424987792969
248 59.184234619140625
249 59.18421936035156
250 59.18425750732422
251 59.184226989746094
252 59.184242248535156
253 59.18424987792969
254 59.184234619140625
255 59.18421936035156
256 59.18425750732422
257 59.184226989746094
258 59.184242248535156
259 59.18424987792969
260 59.184234619140625
261 59.18421936035156
262 59.18425750732422
263 59.184226989746094
264 59.184242248535156
265 59.18424987792969
266 59.184234619140625
267 59.18421936035156
268 59.18425750732422
269 59.184226989746094
270 59.184242248535156
271 59.18424987792969
272 59.184234619140625
273 59.18421936035156
274 59.18425750732422
275 59.184226989746094
276 59.184242248535156
277 59.18424987792969
278 59.184234619140625
279 59.18421936035156
280 59.18425750732422
281 59.184226989746094
282 59.184242248535156
283 59.18424987792969
284 59.184234619140625
285 59.18421936035156
286 59.18425750732422
287 59.184226989746094
288 59.184242248535156
289 59.18424987792969
290 59.184234619140625
291 59.18421936035156
292 59.18425750732422
293 59.184226989746094
294 59.184242248535156
295 59.18424987792969
296 59.184234619140625
297 59.18421936035156
298 59.18425750732422
299 59.184226989746094
300 59.184242248535156
301 59.18424987792969
302 59.184234619140625
303 59.18421936035156
304 59.18425750732422
305 59.184226989746094
306 59.184242248535156
307 59.18424987792969
308 59.184234619140625
309 59.18421936035156
310 59.18425750732422
311 59.184226989746094
312 59.184242248535156
313 59.18424987792969
314 59.184234619140625
315 59.18421936035156
316 59.18425750732422
317 59.184226989746094
318 59.184242248535156
319 59.18424987792969
320 59.184234619140625
321 59.18421936035156
322 59.18425750732422
323 59.184226989746094
324 59.184242248535156
325 59.18424987792969
326 59.184234619140625
327 59.18421936035156
328 59.18425750732422
329 59.184226989746094
330 59.184242248535156
331 59.18424987792969
332 59.184234619140625
333 59.18421936035156
334 59.18425750732422
335 59.184226989746094
336 59.184242248535156
337 59.18424987792969
338 59.184234619140625
339 59.18421936035156
340 59.18425750732422
341 59.184226989746094
342 59.184242248535156
343 59.18424987792969
344 59.184234619140625
345 59.18421936035156
346 59.18425750732422
347 59.184226989746094
348 59.184242248535156
349 59.18424987792969
350 59.184234619140625
351 59.18421936035156
352 59.18425750732422
353 59.184226989746094
354 59.184242248535156
355 59.18424987792969
356 59.184234619140625
357 59.18421936035156
358 59.18425750732422
359 59.184226989746094
360 59.184242248535156
361 59.18424987792969
362 59.184234619140625
363 59.18421936035156
364 59.18425750732422
365 59.184226989746094
366 59.184242248535156
367 59.18424987792969
368 59.184234619140625
369 59.18421936035156
370 59.18425750732422
371 59.184226989746094
372 59.184242248535156
373 59.18424987792969
374 59.184234619140625
375 59.18421936035156
376 59.18425750732422
377 59.184226989746094
378 59.184242248535156
379 59.18424987792969
380 59.184234619140625
381 59.18421936035156
382 59.18425750732422
383 59.184226989746094
384 59.184242248535156
385 59.18424987792969
386 59.184234619140625
387 59.18421936035156
388 59.18425750732422
389 59.184226989746094
390 59.184242248535156
391 59.18424987792969
392 59.184234619140625
393 59.18421936035156
394 59.18425750732422
395 59.184226989746094
396 59.184242248535156
397 59.18424987792969
398 59.184234619140625
399 59.18421936035156
400 59.18425750732422
401 59.184226989746094
402 59.184242248535156
403 59.18424987792969
404 59.184234619140625
405 59.18421936035156
406 59.18425750732422
407 59.184226989746094
408 59.184242248535156
409 59.18424987792969
410 59.184234619140625
411 59.18421936035156
412 59.18425750732422
413 59.184226989746094
414 59.184242248535156
415 59.18424987792969
416 59.184234619140625
417 59.18421936035156
418 59.18425750732422
419 59.184226989746094
420 59.184242248535156
421 59.18424987792969
422 59.184234619140625
423 59.18421936035156
424 59.18425750732422
425 59.184226989746094
426 59.184242248535156
427 59.18424987792969
428 59.184234619140625
429 59.18421936035156
430 59.18425750732422
431 59.184226989746094
432 59.184242248535156
433 59.18424987792969
434 59.184234619140625
435 59.18421936035156
436 59.18425750732422
437 59.184226989746094
438 59.184242248535156
439 59.18424987792969
440 59.184234619140625
441 59.18421936035156
442 59.18425750732422
443 59.184226989746094
444 59.184242248535156
445 59.18424987792969
446 59.184234619140625
447 59.18421936035156
448 59.18425750732422
449 59.184226989746094
450 59.184242248535156
451 59.18424987792969
452 59.184234619140625
453 59.18421936035156
454 59.18425750732422
455 59.184226989746094
456 59.184242248535156
457 59.18424987792969
458 59.184234619140625
459 59.18421936035156
460 59.18425750732422
461 59.184226989746094
462 59.184242248535156
463 59.18424987792969
464 59.184234619140625
465 59.18421936035156
466 59.18425750732422
467 59.184226989746094
468 59.184242248535156
469 59.18424987792969
470 59.184234619140625
471 59.18421936035156
472 59.18425750732422
473 59.184226989746094
474 59.184242248535156
475 59.18424987792969
476 59.184234619140625
477 59.18421936035156
478 59.18425750732422
479 59.184226989746094
480 59.184242248535156
481 59.18424987792969
482 59.184234619140625
483 59.18421936035156
484 59.18425750732422
485 59.184226989746094
486 59.184242248535156
487 59.18424987792969
488 59.184234619140625
489 59.18421936035156
490 59.18425750732422
491 59.184226989746094
492 59.184242248535156
493 59.18424987792969
494 59.184234619140625
495 59.18421936035156
496 59.18425750732422
497 59.184226989746094
498 59.184242248535156
499 59.18424987792969



---------------------------------------------------------------------------

NameError                                 Traceback (most recent call last)

<ipython-input-50-354a79266859> in <module>()
     51 
     52 # After training
---> 53 ytrain_pred = model(x_)


NameError: name 'x_' is not defined